Ever wondered how a simple equation can unlock the secrets of linear relationships? The formula y=mx+b is more than just a mathematical expression; it’s a powerful tool that helps you understand how two variables interact. Whether you’re tackling algebra homework or analyzing data trends, this equation lays the groundwork for grasping essential concepts in math and beyond.
Understanding The Equation Y=MX+B
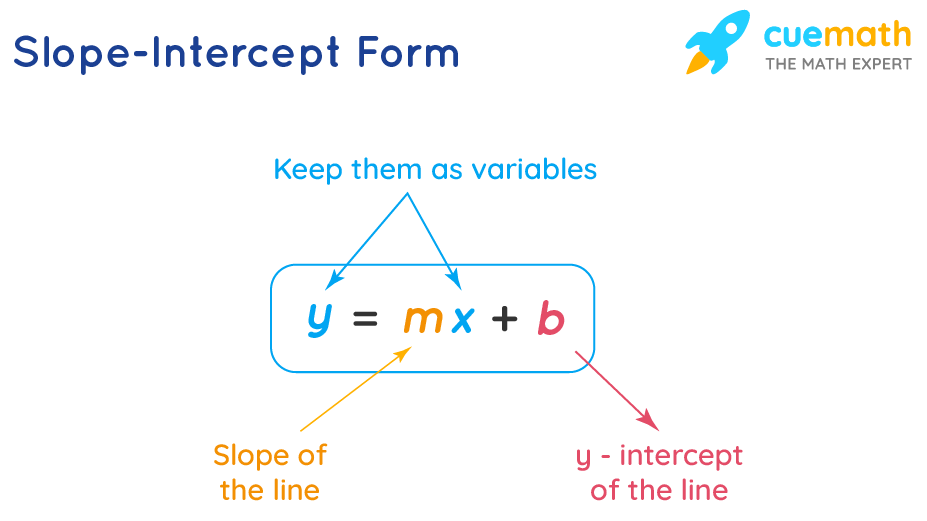
The equation y=mx+b represents a linear relationship between two variables. It serves as a fundamental concept in algebra and is widely used to model various real-life scenarios.
Definition And Components
In the equation y=mx+b, each component plays a crucial role:
- y represents the dependent variable, the output of the function.
- x denotes the independent variable, which you control or manipulate.
- m stands for the slope of the line, indicating how steep it is.
- b signifies the y-intercept, where the line crosses the y-axis when x equals zero.
Understanding these components allows you to grasp how changes in one variable affect another.
Slope And Y-Intercept Explained
The slope (m) measures how much y changes for a unit change in x. A positive slope indicates an upward trend, while a negative slope shows a downward trend. For instance:
- If m = 2, then every time x increases by 1, y increases by 2.
- If m = -3, then every time x increases by 1, y decreases by 3.
The y-intercept (b) tells you where your line starts on the graph. For example:
- If b = 4, your line crosses the y-axis at (0,4).
- If b = -1, your line intersects at (0,-1).
Both elements are vital for graphing linear functions and interpreting data trends effectively.
Applications Of Y=MX+B
The equation y=mx+b finds numerous applications in various fields, providing essential insights into relationships between variables. Understanding these applications can enhance your grasp of linear functions and their significance.
Real-World Examples
You encounter y=mx+b in everyday situations. For instance:
- Finance: In budgeting, the cost function might represent fixed expenses (b) plus variable costs per item (m).
- Physics: The equation models speed as distance over time, where the slope indicates velocity.
- Economics: Supply and demand graphs use this formula to illustrate price changes relative to quantity supplied or demanded.
These examples demonstrate how widely applicable this equation is across different domains.
Importance In Algebra And Beyond
In algebra classes, mastering y=mx+b is crucial for solving linear equations. You’ll apply it when graphing lines on a coordinate system or analyzing data sets.
Moreover, its relevance extends beyond academics:
- Data Analysis: Businesses rely on regression analysis to predict trends.
- Engineering: Engineers use the equation to design structures that meet specific criteria.
Graphing Y=MX+B
Graphing the equation y=mx+b involves visualizing a linear relationship between two variables. You plot the line based on its slope and y-intercept, which provides key insights into how one variable affects another.
Step-By-Step Guide
- Identify the components: Recognize that m represents the slope, while b indicates where the line crosses the y-axis.
- Plot the y-intercept: Start by marking point (0,b) on the graph.
- Use the slope: From your y-intercept, use m to determine how to move up or down and left or right to find a second point. For example, if m = 2, go up 2 units for every 1 unit you move right.
- Draw the line: Connect these points with a straight line extending in both directions.
This method ensures an accurate representation of your linear equation.
- Forgetting to label axes: Always label your x and y axes clearly to avoid confusion.
- Incorrectly calculating slope: Double-check how you interpret m; remember it indicates rise over run.
- Neglecting negative slopes: A negative value for m means your line will slant downward from left to right; be mindful of this when plotting.
- Overcomplicating points: Stick with simple integers for ease of plotting; complex numbers can lead to errors.
Avoiding these pitfalls makes graphing more straightforward and effective.
Variations And Extensions
The equation y=mx+b has several variations and extensions that enhance its application in different contexts. Understanding these modifications allows you to utilize the linear model more effectively.
Modifications Of The Linear Equation
Modifying the standard form of y=mx+b often tailors it for specific scenarios. For example, when working with multiple variables, you can extend it to:
- y = m1x1 + m2x2 + b: This represents a situation involving two independent variables.
- y = mx + c: In this case, ‘c’ might substitute ‘b,’ emphasizing a different intercept.
These adaptations enable analysis of more complex relationships in data sets. Isn’t it fascinating how a simple formula can accommodate such versatility?
Non-Linear Relationships
While y=mx+b focuses on linear relationships, many real-world situations involve non-linear patterns. You might encounter quadratic equations like y = ax² + bx + c, which represent parabolic relationships.
Consider these examples:
- Population growth often follows an exponential curve rather than a straight line.
- Projectile motion can be modeled using quadratic functions due to acceleration effects.
Understanding non-linear models is crucial for analyzing trends accurately. By recognizing these distinctions, you improve your analytical skills significantly.