Imagine navigating the world without a clear direction. Vectors are your guiding stars in mathematics and physics, providing both magnitude and direction to help you understand complex concepts. Whether you’re plotting a course on a map or analyzing forces in engineering, vectors play an essential role.
In this article, you’ll explore various examples of vectors that illustrate their importance in real-life applications. From the simple act of walking to the intricate workings of technology like GPS, understanding vectors can transform how you perceive movement and force. Have you ever wondered how video games create realistic motion? Vectors are at the heart of it all.
Get ready to dive deep into the fascinating world of vectors as we uncover their significance across different fields and everyday scenarios. You’ll gain insights that not only enhance your knowledge but also spark curiosity about how these mathematical tools shape our reality.
Understanding Vectors
Vectors play a crucial role in various fields, from mathematics to everyday activities. They provide both magnitude and direction, making them essential for understanding physical concepts.
Definition and Importance
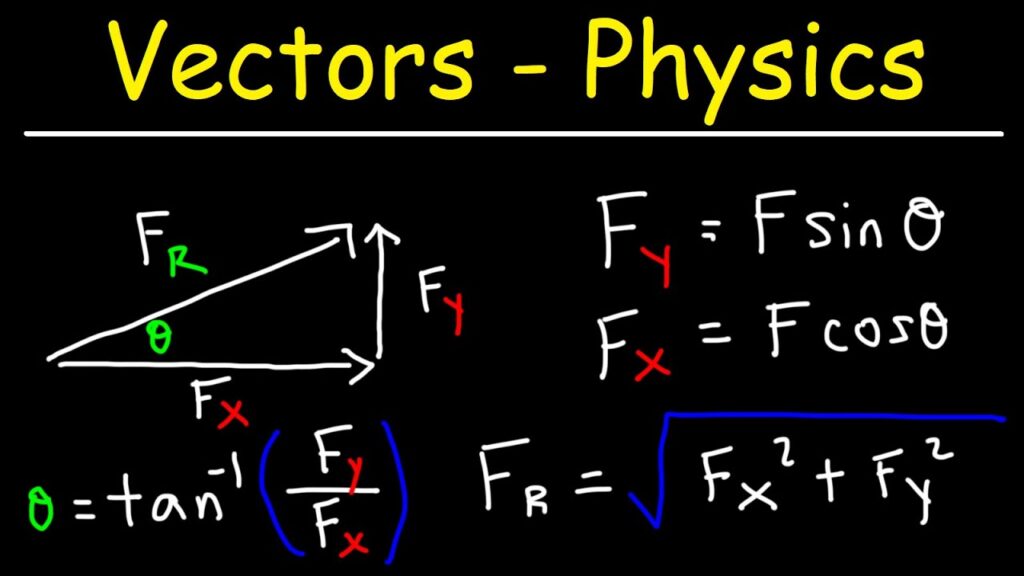
A vector is a mathematical object characterized by its magnitude (length) and direction (orientation). For example, when you walk 3 miles north, your movement can be represented as a vector with a length of 3 miles pointing north. This dual nature makes vectors vital in physics, engineering, and even computer graphics. By using vectors, you gain clarity on how forces act or how objects move in space.
Types of Vectors
There are several types of vectors you might encounter:
- Position Vectors: Indicate the location of a point relative to an origin.
- Displacement Vectors: Represent the change in position from one point to another.
- Velocity Vectors: Show the speed and direction of moving objects.
- Force Vectors: Illustrate the application of force acting on an object.
Each type serves specific purposes across different applications. For instance, velocity vectors help understand how fast something moves in what direction—essential for navigation systems like GPS.
Mathematical Representation of Vectors
Vectors are represented mathematically to convey both their magnitude and direction clearly. The notation used for vectors simplifies operations and calculations in various applications.
Vector Notation
Vectors typically appear in boldface, such as v, or with an arrow above the letter, like (vec{v}). For example, a vector representing a force might be denoted as F or (vec{F}). Components of vectors often use rectangular coordinates. A 2D vector can be expressed as ((x, y)), where (x) represents the horizontal component and (y) represents the vertical component. In three dimensions, it’s noted as ((x, y, z)).
Operations on Vectors
You can perform several operations on vectors that enhance their utility in mathematics and physics:
- Addition: To add two vectors A and B, sum their corresponding components:
- If A = (1, 2) and B = (3, 4), then A + B = (1+3, 2+4) = (4, 6).
- Subtraction: Subtract one vector from another by subtracting each component:
- If C = (5, 7) and you want to find C – A, then calculate it as (5-1, 7-2) = (4, 5).
- Scalar Multiplication: Multiply a vector by a scalar to scale its magnitude without changing its direction:
- If you multiply vector D = (2, 3) by a scalar of (k=2), then (k * D) gives you (22, 32) = (4, 6).
These operations provide essential tools for solving problems involving motion and forces. Understanding how to manipulate vectors leads to better insights into physical phenomena in your daily life.
Applications of Vectors
Vectors play a crucial role in various fields, influencing both daily activities and advanced technologies. You can encounter these applications in numerous areas, including physics, engineering, and computer graphics.
Physics and Engineering
In physics and engineering, vectors represent quantities that have both magnitude and direction. For example, the force exerted on an object is expressed as a vector. This helps engineers design structures by calculating loads accurately.
Another instance involves velocity vectors; they describe how fast an object moves in a specific direction. When analyzing projectile motion, understanding velocity vectors allows for precise predictions of trajectories. Additionally, displacement vectors indicate changes in position over time; they’re essential in navigation systems and robotics.
Computer Graphics
In computer graphics, vectors define shapes and movements within digital environments. For instance, graphical objects are represented using position vectors to determine their coordinates on the screen.
Furthermore, transformation operations like rotation or scaling rely heavily on vector mathematics. An object’s orientation changes based on vector manipulation during animation sequences. When you interact with 3D models or video games, it’s vectors that create realistic motions and perspectives.
Common Misconceptions About Vectors
Misunderstandings about vectors can lead to confusion, especially regarding their characteristics and applications. Addressing these misconceptions clarifies the concept and enhances your understanding.
Misunderstanding Direction
Many people think direction in vectors is arbitrary, but it’s not. Direction significantly affects vector representation and interpretation. For instance, if you walk 5 miles east versus 5 miles west, those movements represent different vectors despite having the same magnitude. This difference shows how crucial direction is when working with vectors in navigation or physics.
Confusion with Scalars
Some often confuse vectors with scalars due to their similar appearances in equations. Vectors contain both magnitude and direction, while scalars only have magnitude. A classic example includes speed versus velocity; speed measures how fast something moves (a scalar), whereas velocity specifies the object’s speed along with its direction (a vector). Understanding this distinction helps clarify concepts in physics and engineering where precise measurements are critical.