Imagine standing at a point where two paths diverge in opposite directions. This is the essence of opposite rays, a fundamental concept in geometry that can enhance your understanding of lines and angles. But what exactly are opposite rays, and why do they matter?
Definition of Opposite Rays
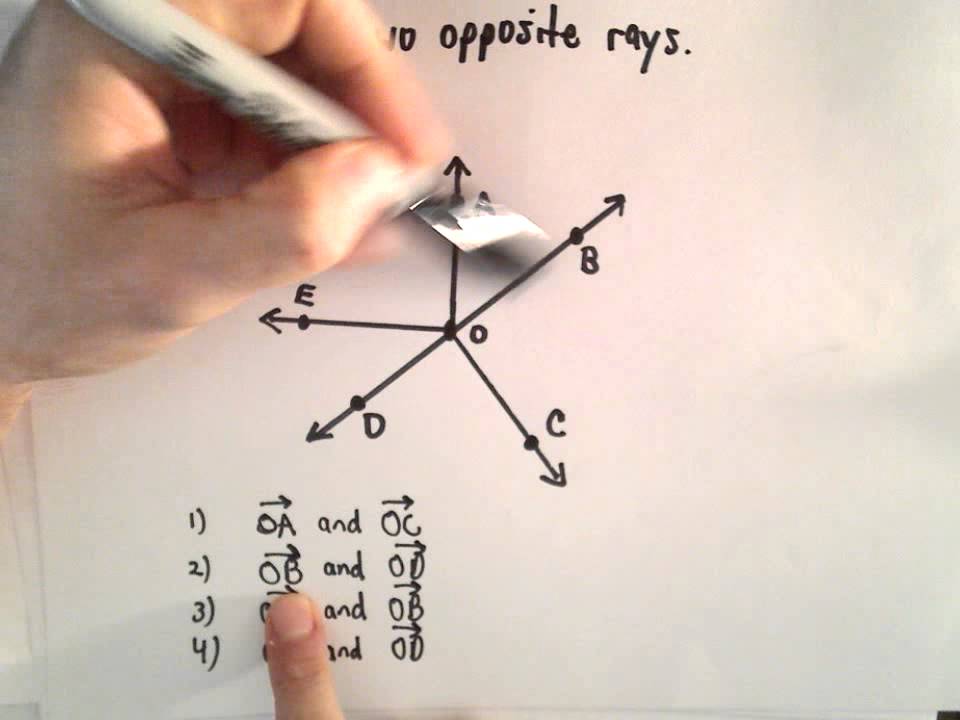
Opposite rays are an essential concept in geometry. They consist of two rays that share a common endpoint, extending infinitely in opposite directions.
Characteristics of Opposite Rays
- Common Endpoint: Both rays begin at the same point, which serves as their starting location.
- Infinite Extension: Each ray extends endlessly without ending, forming straight lines.
- Linear Relationship: The two rays create a straight line when combined, highlighting their linear nature.
- Angle Formation: Together, opposite rays form an angle measuring 180 degrees.
Visual Representation
Visualizing opposite rays is crucial for understanding their structure. In diagrams:
- A single point represents the common endpoint.
- Two arrows indicate the direction of each ray extending from this point.
- The illustration shows both arrows moving away from each other along a straight line.
This clear representation helps one grasp how opposite rays function within geometric contexts.
Examples of Opposite Rays
Opposite rays appear in various contexts, making them easier to understand. Here are some clear examples to illustrate the concept.
Everyday Examples
- Sunrise and Sunset: Picture a straight line from the horizon at sunrise to the horizon at sunset. Each point represents an opposite ray extending infinitely in both directions.
- Road Intersection: Consider a road that splits into two paths at an intersection. The point where they meet acts as the common endpoint for both opposite rays.
- Bicycle Paths: Imagine two bicycle lanes diverging from a single park entrance. Each lane extends away from each other, representing opposite rays originating from that entry point.
- Coordinate Plane: In geometry, if you take point O(0, 0) on a coordinate plane, then points A(1, 1) and B(-1, -1) form opposite rays OA and OB extending endlessly along their respective lines.
- Angle Bisector: If you draw a line segment with endpoints A and B creating angle C, then rays CA and CB are considered opposite rays since they extend in opposing directions from point C.
| Example | Description |
|---|---|
| Sunlight Direction | Rays extending outwards from the sun |
| Line Segments | Points on a number line showing infinite extension |
| Geometry Problems | Angles formed by intersecting lines |
Understanding these examples helps reinforce how opposite rays function within geometry and everyday life.
Properties of Opposite Rays
Opposite rays exhibit distinct properties that are crucial for understanding their role in geometry. These properties emphasize their structure and function.
Relation to Angles
Opposite rays create a straight angle, measuring 180 degrees. When two rays extend in opposite directions from a common point, they form this specific angle. For instance, if you visualize the sun setting and rising at different times of the day, these scenarios represent opposite rays emanating from a single point on the horizon. This relationship aids in identifying linear pairs of angles formed when two lines intersect.
Importance in Geometry
Understanding opposite rays is essential for grasping more complex geometric concepts. They establish foundational relationships between points and lines. Here are key aspects:
- Common Endpoint: Each pair shares a starting point.
- Infinite Extension: Rays continue infinitely without end.
- Straight Line Formation: Together, they create a complete line.
These characteristics highlight how opposite rays contribute to constructing geometric figures and solving problems involving angles and lines effectively.
Applications of Opposite Rays
Opposite rays find significant applications in various fields, particularly in geometry and everyday contexts. Their unique properties help illustrate key concepts.
In Geometry
In geometry, opposite rays play a crucial role in understanding angles and lines. For example:
- Formation of Straight Angles: When two opposite rays originate from a single point, they create a straight angle measuring 180 degrees.
- Linear Pairs: When two lines intersect, the pairs of adjacent angles formed can be analyzed through opposite rays.
- Coordinate Systems: In a Cartesian plane, opposite rays define directions from an origin point to extend infinitely.
These examples highlight how essential opposite rays are for constructing geometric figures and solving related problems effectively.
In Real-Life Scenarios
You can observe opposite rays in numerous real-life situations. Consider these examples:
- Sunrise and Sunset: The sun’s path creates two opposing rays extending from the horizon during sunrise or sunset.
- Road Intersections: When roads diverge at an intersection, each road represents an opposite ray extending indefinitely from the common point.
- Bicycle Paths: Paths branching out from a park entrance act as opposite rays leading into different directions.
Such scenarios illustrate that while you may not notice them daily, opposite rays significantly impact your environment.