Ever wondered why some relationships just don’t qualify as functions? Understanding not a function examples can clarify this concept and sharpen your mathematical skills. Functions are all about unique inputs leading to single outputs, but what happens when that rule gets broken?
Understanding Functions
A function in mathematics is a specific relationship where each input corresponds to exactly one output. This unique pairing ensures clarity and predictability in mathematical operations. However, not all relationships qualify as functions. Here are some examples of relationships that do not meet the criteria for functions:
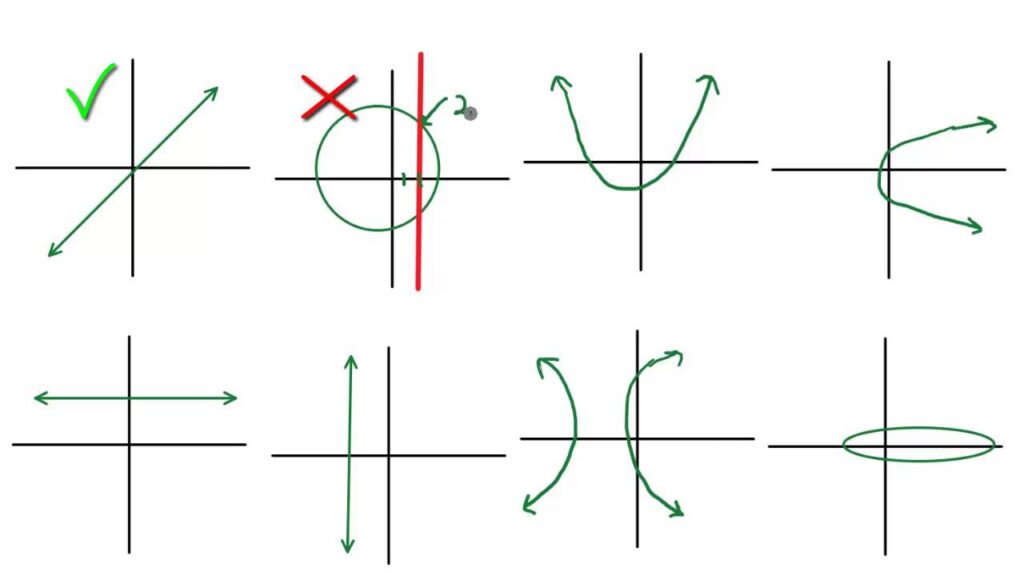
- Vertical Line Test: If you can draw a vertical line through a graph and it intersects more than once, the relation isn’t a function.
- Multiple Outputs: When one input yields several outputs, such as (x^2 = 4) (where both (2) and (-2) work), this setup lacks functionality.
- Set of Ordered Pairs: Consider the set {(1, 2), (1, 3)}. The input (1) links to two different outputs, making it not a function.
These examples highlight common scenarios that illustrate why certain relationships don’t qualify as functions. Understanding these distinctions aids your grasp of mathematical concepts and enhances problem-solving skills.
Common Characteristics of Functions
Functions exhibit specific characteristics that differentiate them from other relationships. A function pairs each input with one unique output, ensuring clarity in mathematical operations. Recognizing whether a relationship meets these criteria simplifies problem-solving and enhances understanding.
One-to-One Functions
One-to-one functions assign exactly one unique output to every input. In other words, no two distinct inputs can produce the same output. For example, the function f(x) = 2x is one-to-one because each x corresponds to a different value of f(x). You can easily verify this by checking ordered pairs like (1, 2) and (2, 4); they illustrate the uniqueness clearly.
Many-to-One Functions
Many-to-one functions allow multiple inputs to share the same output. This means that different values can lead you to the same result. For instance, the function g(x) = x² demonstrates this characteristic since both -3 and 3 yield an output of 9. It’s essential to identify many-to-one relationships as they often appear in real-world scenarios like calculating areas or volumes where varying dimensions might result in identical outcomes.
What Is Not a Function?
Not every relationship between inputs and outputs qualifies as a function. A function requires that each input corresponds to exactly one output. If an input leads to multiple outputs, it falls outside the definition of a function.
Vertical Line Test
The vertical line test serves as a visual method to determine if a graph represents a function. If any vertical line intersects the graph at more than one point, the relationship isn’t a function. This simple check helps identify non-functions quickly by looking at graphs rather than equations.
Examples of Not a Function
Several specific examples illustrate relationships that do not meet the criteria for functions:
- Vertical Line Intersection: Any graph where you can draw vertical lines intersecting at two points indicates it’s not a function.
- Multiple Outputs for One Input: For instance, the equation (x^2 = 4) has two solutions: (2) and (-2). Here, input (x = 2) gives different outputs.
- Ordered Pairs Issue: The set ({(1, 2), (1, 3)}) shows that input (1) results in both (2) and (3), disqualifying it as a function.
- Circle Equation Example: The equation of a circle such as (x^2 + y^2 = r^2) fails since various values of (y) correspond to single values of (x).
Recognizing these instances enhances your understanding of mathematical functions and their properties.
Real-World Applications
In various real-world situations, you encounter relationships that don’t qualify as functions. Understanding these examples helps clarify mathematical concepts.
- Street Mapping: When mapping streets, multiple routes can connect the same destination. For instance, both Route A and Route B might lead to the same address. Each starting point doesn’t guarantee a unique endpoint.
- Employee Roles: In an organization, one employee can perform multiple roles simultaneously. If Jane is both a manager and a trainer, her responsibilities overlap in ways that complicate role assignments.
- Sports Statistics: An athlete’s performance may yield different statistics for various games. A player could score 30 points in one game and 15 in another; thus, their average isn’t tied to a single input.
- Weather Forecasting: Predicting weather involves numerous variables like humidity and temperature affecting outcomes differently each day. One set of conditions doesn’t dictate precise weather results.
- Production Processes: In manufacturing, several machines might produce the same product type but with varying quality levels based on settings or materials used—creating inconsistencies in output for identical inputs.
Recognizing these examples of non-functions strengthens your grasp on how mathematical principles apply to everyday scenarios.