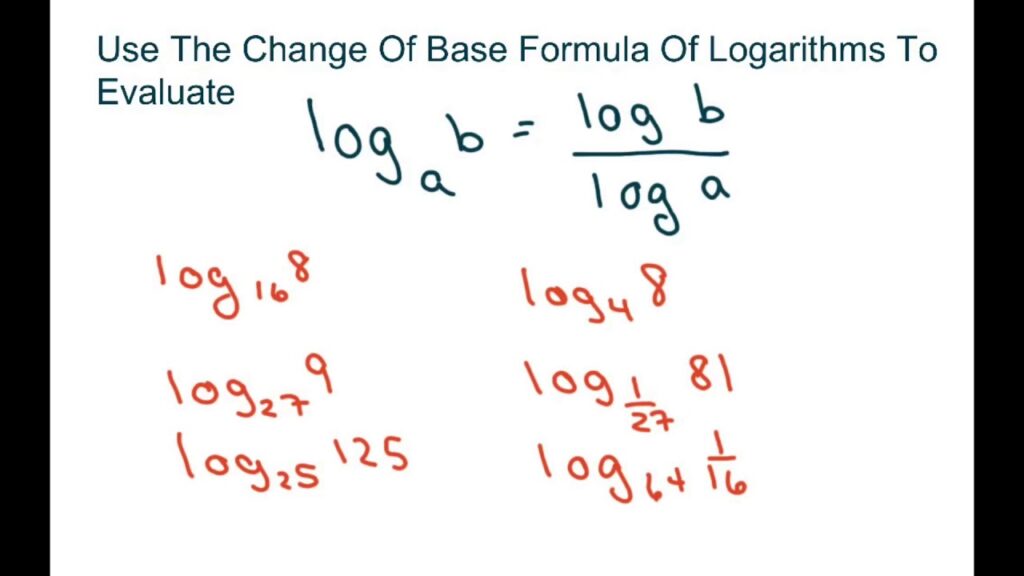Have you ever found yourself struggling with logarithms in different bases? Understanding the log change of base can simplify your calculations and enhance your math skills. This powerful technique allows you to convert logarithms from one base to another effortlessly, making it easier to solve complex equations.
Overview of Logarithms
Logarithms simplify the process of solving exponential equations. They provide a way to express large numbers in a more manageable form, making calculations easier.
Definition of Logarithms
A logarithm answers the question: “To what exponent must a certain base be raised to produce a given number?” For example, in the expression ( log_b(a) = c ), this means that ( b^c = a ). If you take ( log_{10}(100) ), it equals 2 because ( 10^2 = 100 ).
Importance of Logarithms in Mathematics
Logarithms play a crucial role in various mathematical fields. They help:
- Simplify complex calculations: Using logs can turn multiplication into addition and division into subtraction.
- Model real-world phenomena: Logs appear in growth models like population growth or radioactive decay.
- Solve exponential equations: Logs provide methods for finding unknown variables when dealing with exponents.
Understanding logarithms enhances your problem-solving skills and allows for deeper engagement with mathematical concepts.
Log Change of Base Explained
Logarithms can seem complex, but the log change of base makes them easier to handle. This technique simplifies calculations across different bases and enhances your mathematical skills.
The Change of Base Formula
The change of base formula allows you to convert logarithms from one base to another. It states:
[
log_b(a) = frac{log_k(a)}{log_k(b)}
]
Here, (b) is the original base, (a) is the number, and (k) is any new base you choose (commonly 10 or (e)). For example, if you want to find (log_2(8)), using base 10:
[
log_2(8) = frac{log_{10}(8)}{log_{10}(2)} approx frac{0.903}{0.301} = 3
]
This shows that changing bases can lead to simpler calculations.
Derivation of the Change of Base Formula
To derive the change of base formula, start with the definition of a logarithm:
If (y = log_b(a)), then by definition we have:
[
b^y = a
]
Now take logarithm in any new base, say (k):
[
k^{(log_k(b^y))} = k^{(log_k(a))}
]
Using properties of exponents and logs:
[
y cdot log_k(b) = log_k(a)
]
Rearranging gives us:
[
y = frac{log_k(a)}{log_k(b)}
]
This derivation confirms why this formula works for converting between bases seamlessly.
Applications of Log Change of Base
Log change of base simplifies calculations and enhances problem-solving skills in various mathematical contexts. Understanding its applications can improve efficiency when working with logarithms.
Simplifying Logarithmic Expressions
Using the log change of base technique allows you to convert complex logarithmic expressions into simpler forms. For example, consider (log_2(16)). You can use the change of base formula:
[
log_2(16) = frac{log_{10}(16)}{log_{10}(2)}
]
Calculating this yields approximately (4), as (2^4 = 16). This method streamlines difficult expressions and makes them more manageable.
Solving Logarithmic Equations
Log change of base is essential for solving logarithmic equations effectively. Suppose you need to solve (3^x = 81). First, rewrite it using logarithms:
[
x = log_3(81)
]
Apply the change of base formula:
[
x = frac{log_{10}(81)}{log_{10}(3)}
]
Calculating this gives approximately (4), since (3^4 = 81). This approach not only clarifies the solution but also saves time during calculations.
Utilizing these applications can significantly enhance your understanding and ability to work with logarithms efficiently.
Common Mistakes and Misunderstandings
Understanding logarithms can be tricky. Here are common mistakes and misunderstandings that often occur with the log change of base.
Misapplying the Change of Base Formula
Many people incorrectly apply the change of base formula, (log_b(a) = frac{log_k(a)}{log_k(b)}). For example, if you calculate (log_2(8)) using the incorrect base or fail to simplify correctly, you might end up with an inaccurate result. Remember to choose a consistent base for both parts of the formula.
Confusion Between Different Bases
Confusion arises when switching between bases. You might think that (log_{10}(100)) equals (log_2(100)), but that’s not correct. Each logarithm depends on its specific base. To clarify:
- Base 10: (log_{10}(100) = 2)
- Base 2: (log_2(100) ≈ 6.64)
This difference highlights why understanding each logarithm’s context is crucial.