Have you ever wondered how to find balance in shapes? The line of symmetry equation is your key to uncovering the hidden beauty of geometric figures. This concept isn’t just a mathematical curiosity; it plays a crucial role in art, design, and nature. Understanding this equation can help you analyze patterns and create visually appealing designs.
Overview Of Line Of Symmetry
The line of symmetry refers to a line that divides a shape into two identical parts. This concept applies across various fields, including geometry and art. Understanding this principle enhances your ability to analyze shapes and designs effectively.
For example, consider basic geometric shapes:
- Circle: Any diameter serves as a line of symmetry.
- Square: Four lines of symmetry exist—two diagonals and two perpendicular bisectors.
- Rectangle: It has two lines of symmetry along its length and width.
Also, in nature, you can observe lines of symmetry in flowers. For instance, many flowers exhibit radial symmetry with multiple identical petals around a center point.
Art also leverages the idea. Artists often use symmetrical balance for aesthetic appeal. Think about famous works like the Mona Lisa; they exhibit vertical symmetry through the central axis.
Identifying these lines not only helps in mathematics but also enhances your design skills throughout various projects.
Importance Of Line Of Symmetry
The line of symmetry plays a crucial role in various fields, enhancing both understanding and application. It simplifies complex shapes while promoting balance and aesthetics.
Applications In Geometry
In geometry, the line of symmetry aids in shape analysis. For instance:
- Triangles can have one or more lines of symmetry depending on their type.
- Rectangles possess two lines of symmetry—one vertical and one horizontal.
- Circles exhibit infinite lines of symmetry, radiating from the center to any point on the perimeter.
These applications allow you to easily determine congruence and properties within geometric figures.
Real-World Examples
You encounter lines of symmetry everywhere in daily life. Consider these examples:
- Architectural designs, like buildings with symmetrical facades.
- Nature, such as butterflies that showcase bilateral symmetry.
- Artworks, where artists employ symmetry for visual harmony—think about famous pieces like Da Vinci’s work.
Recognizing these instances not only reinforces mathematical concepts but also enriches your appreciation for beauty in design.
Understanding The Line Of Symmetry Equation
The line of symmetry equation plays a crucial role in various mathematical and real-world applications. This equation helps determine the precise location of symmetry within shapes, facilitating easy analysis.
Definition And Explanation
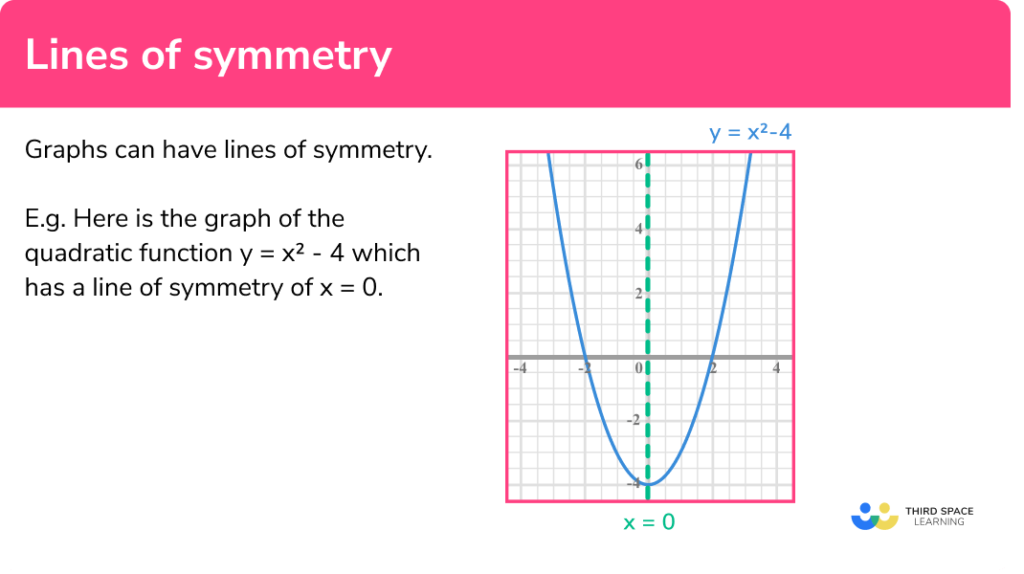
The line of symmetry refers to an imaginary line that divides a shape into two identical halves. If you fold a shape along this line, both sides match perfectly. For example, in a rectangle, the vertical and horizontal lines serve as lines of symmetry. Moreover, understanding this concept enhances your ability to analyze geometric figures effectively.
Types Of Symmetry
Symmetry can manifest in different forms within shapes:
- Bilateral Symmetry: Found in objects like butterflies or human faces; one side mirrors the other.
- Radial Symmetry: Commonly seen in flowers; parts radiate from a central point.
- Reflective Symmetry: Exists when one half is a reflection of the other half across a specific line.
Recognizing these types reinforces your mathematical skills while also appreciating patterns in nature and design.
How To Determine The Line Of Symmetry
Determining the line of symmetry involves a few straightforward steps. By following these guidelines, you can easily identify symmetrical lines in various shapes.
Steps For Finding The Equation
- Identify the Shape: Recognize whether you’re dealing with geometric figures like triangles, rectangles, or circles.
- Visualize the Shape: Draw or visualize the shape to understand its structure better.
- Locate Points: Pinpoint key points on the shape that will help in finding symmetry.
- Draw Potential Lines: Sketch potential lines of symmetry through those key points.
- Check for Reflection: Fold or reflect the shape along those lines to see if both halves match perfectly.
For example, a rectangle has two lines of symmetry: one vertical and one horizontal.
- Forgetting to check all possible lines can lead to missed symmetries.
- Assuming that all shapes have an equal number of symmetrical lines isn’t accurate; each shape varies.
- Overlooking irregular shapes may cause confusion; always analyze their unique features closely.
By staying aware of these pitfalls, you enhance your ability to determine lines of symmetry accurately across different figures.